©Copyright 2021 Columbine of Maine, all rights reserved Permission is given to individuals to keep copies of these.
- Hohmann Transfer Orbit For a small body orbiting another very much larger body, such as a satellite orbiting the earth, the total energy of the smaller body is Velocity equation where: is the speed of an orbiting body is the standard gravitational parameter of the primary body.
- For the Hohmann transfer, we demand that: Rearranging, the required fractional change in velocity from the first impulse is So we can get the rocket to reach the height for an instant, but we need a second impulse to keep it there and circularise the orbit. Say this requires an additional change in velocity.
- Let’s say you wanted to go to Mars, The transfer orbit, orbits the Sun. It is highly elliptical and has a low point that is as close to the Sun as Earth and the highest point as close to the Sun as Mars.
Hohmann transfers are not just for Earth orbiting spacecraft - they can also be used for interplanetary transfers. Calculating an interplanetary Hohmann transfer is very similar to calculating a Hohmann transfer for an Earth orbiting spacecraft. The only difference we have is that we have one more thing to calculate: The necessary phase angle for the two planets.
In this section, we will cover:
1.Calculating an Interplanetary Hohmann Transfer
2.Modeling an Interplanetary Hohmann Transfer
Calculating an Interplanetary Hohmann Transfer
Calculating the Δv required for an interplanetary Hohmann transfer is exactly like how we did it in the Hohmann Transfer tutorial. Our 'parking' orbit SMA is actually our departure planet's SMA about the Sun. Our 'target' orbit SMA is the arrival planet's SMA about the Sun.
However, like the Hohmann Transfer tutorial, we must assume that the two planets are both circular and co-planar. Since this definitely isn't the case with any of our solar system's planets in the real world, these calculations only present a conceptual idea of the amount of Δv required for an interplanetary transfer.
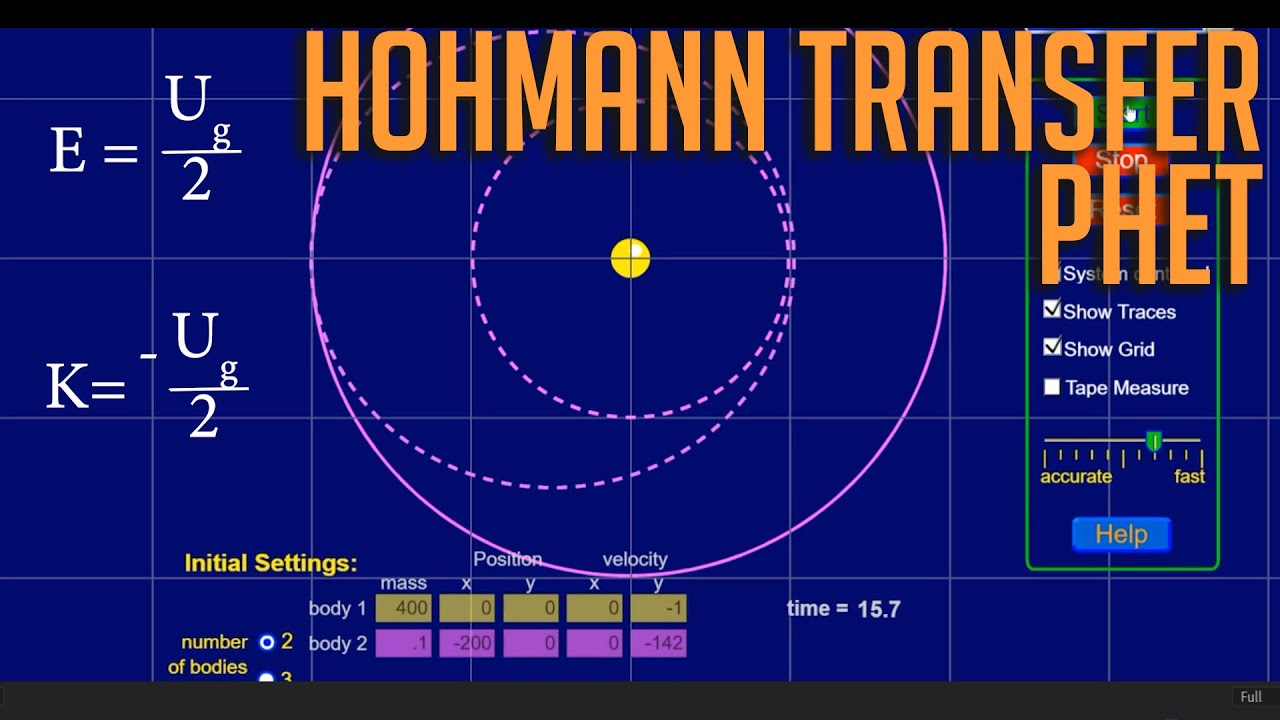
One more thing we need to do in addition to the Δv calculations is calculating the necessary phase angle between the planets. The planets need to be at a certain position relative to each other so that when the interplanetary spacecraft reaches the other side of the Hohmann transfer, the arrival planet is there as well. The phase angle 'Φ' is shown here:
Phase Angle Diagram
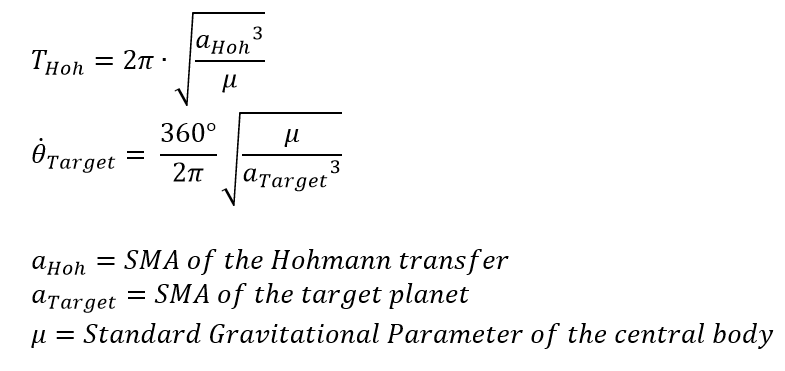
You can calculate the phase angle using the following formula:
For this formula, you need the period of the Hohmann transfer, and the angular velocity of the target planet. What we are essentially doing is finding how many degrees the target planet will travel during the time of the Hohmann transfer, which is half of the Hohmann transfer period. To calculate the period of the Hohmann transfer and the angular velocity of the target orbit, we need the following formulas:
It is important to note that the formula for the angular velocity is only true when dealing with a circular orbit. Because our interplanetary Hohmann transfer assumes a perfectly circular orbit for both planets, we can use this formula.
Modeling an Interplanetary Hohmann Transfer
When calculating Hohmann transfers, we must first assume that both orbits are circular. In the real world, the orbits of Earth and Mars are not circular. So to model an interplanetary Hohmann transfer, we will be using Spacecraft in heliocentric circular orbits with the same SMA as the planets they are representing. Because basic interplanetary Hohmann transfers only rely on the gravity of the central body, we do not need to model the departure and arrival planets' gravities in our problem.
Problem: Assume that Earth and Mars are in circular orbits around the Sun at 1 AU and 1.524 AU, respectively. How much Δv is required to perform a Hohmann transfer to Mars? How many days would this transfer take? |
•Create a new Mission Plan and save it as 'InterplanetaryHohmann.MissionPlan'
Adding in Spacecraft
•Create a Spacecraft with the following elements:
oCentral Body: 'Sun'
Behringer inuke dsp software. oReference Frame: 'Mean of J2000 Earth Ecliptic'
oA: 149,597,871 km (This is 1 AU)
oE: 0
oI: 0 deg
oRAAN: 0 deg
oW: 0 deg
oTA: 0 deg
NOTE: Remember that you need to change the Element Type to 'Keplerian' to access these elements
•Rename the Spacecraft to 'InterplanetarySC'
•Click on the 'Force Model' on the left-hand side
•Uncheck the 'Earth' and 'Moon' boxes
•Click on 'Propagator' on the left-hand side
•Change the step size to 1 day
•Click 'Ok' to close the editor
•Clone 'InterplanetarySC'
•Rename the clone to 'MarsSC' (this Spacecraft will represent Mars)
•Change A to 227,987,155 km (This is 1.524 AU)
•Click on 'Visualization' on the left-hand side
•Change the tail color to green
•Click 'Ok' to close the editor
Adding in the ViewWindow
•Create a ViewWindow through the Object Browser
•Double click on 'ViewWindow1' to open the editor
•Check each Spacecraft in the 'Available Objects'
•Click on 'Spacecraft' in the 'Available Objects' to select both Spacecraft, then check 'Show Name'
•Change the history mode to 'Unlimited' (for both Spacecraft)
Since we won't be needing to show the real Earth and the real Mars, let's hide them from the ViewWindow.
•Click on the 'Solar System' section on the left-hand side
•Click on 'Earth'
•Uncheck 'Show Object' in 'Object Options'
•Click on 'Mars'
•Uncheck 'Show Object' in 'Object Options'
Solar System Properties in the ViewWindow Editor

Now we can continue with the rest of the settings for the ViewWindow.
•Click on 'Viewpoints' on the left-hand side
•Change the reference frame to 'Inertial'
•Change the Source to 'Sun'
•Click 'Copy to Target/Tail Ref.'
•In 'Source Offsets', change the radius to 500,000,000 km
•Click 'Ok' to close the editor
Adding an ImpulsiveBurn
•Create an ImpulsiveBurn object through the Object Browser
•Double-click on 'ImpulsiveBurn1' to open the editor
•Change the attitude system to 'VNB'
•Click 'Ok' to close the editor
Building the Mission Sequence
To start, we'll propagate the entire solar system for a while so we can see each planet's orbit better.
•Drag and drop a while loop into the Mission Sequence
•Change the while loop argument to '(InterplanetarySC.ElapsedTime < TIMESPAN(500 days))'

•Drag and drop a FreeForm script editor inside that while loop
•Open the script editor and rename it to 'Step and Update'
In this script, we will step both Spacecraft with an epoch sync, and update the ViewWindow. To do this, we write:
// Steps both spacecraft with an epoch sync Step InterplanetarySC; Step MarsSC to (MarsSC.Epoch InterplanetarySC.Epoch); // Updates the ViewWindow Update ViewWindow1; |
Let's go back to the Mission Sequence.
•Drag and drop a FreeForm script editor after the while loop
•Open the script editor and rename it to 'Calculate Hohmann Delta V'
In this FreeForm script editor, we will calculate the necessary Δv needed and assign it to the ImpulsiveBurn object we created. To do this, we write:
// SMAs of the departure and arrival planets Variable startingOrbit = InterplanetarySC.A; Variable arrivalOrbit = MarsSC.A; // SMA of the Hohmann transfer Variable transfSMA = (startingOrbit + arrivalOrbit)/2; // Velocity of the Hohmann transfer at Periapsis Variable vTransfPeri = sqrt(Sun.Mu * ((2/startingOrbit) - (1/transfSMA))); // Delta V for the Hohmann transfer Variable dV1 = vTransfPeri - InterplanetarySC.VMag; ImpulsiveBurn1.BurnDirection[0] = dV1; |
Next, we need to calculate the phase angle. Let's add another FreeForm script editor to the Mission Sequence.
•Drag and drop a FreeForm script editor after the 'Calculate Hohmann Delta V' FreeForm
•Open the script editor and rename it to 'Calculate Phase Angle'
In this script, we need to calculate the necessary phase angle for the Hohmann transfer. To do this, we can use the formulas given in the Calculating an Interplanetary Hohmann Transfer section. We will need to write:
Variable Pi = acos(-1); // Period of the Hohmann transfer Variable THoh = 2 * Pi * sqrt(transfSMA^3/Sun.Mu); // Angular Velocity of the Target Planet Variable angVelTarget = (360/(2 * Pi)) * sqrt(Sun.Mu/(arrivalOrbit^3)); // Phase Angle Variable phaseAngle = 180 - (1/2) * (THoh * angVelTarget); |
Now that we've calculated the phase angle, we should try and calculate another very helpful thing: the next epoch at which this phase angle occurs. To do this, we will need to calculate two things: the current phase angle, and the phase angular velocity (the rate at which the phase angle changes).
The current phase angle is pretty easy to calculate. If we take the position vectors of each Spacecraft and use the 'VertexAngle' method, we can calculate the angle between the two.
// Current Phase Angle Variable currentPhaseAngle = InterplanetarySC.Position.VertexAngle(MarsSC.Position); |
However, this method will not return a value greater than 180 degrees. If Earth is ahead of Mars, we need to add 180 degrees to the phase Angle. To do this, we can take the z component of the cross product of InterplanetarySC.Position and MarsSC.Position, and check to see if it's negative. If it is, that means we need to add 180 degrees. To do this, we write:
// If Earth is in front of Mars, add 180 degrees to the current phase angle If(InterplanetarySC.Position.CrossProduct(MarsSC.Position)[2] < 0) then; currentPhaseAngle += 180; End; |
Now, we need to calculate the phase angular velocity. In this scenario, this will simply be the difference between Earth's angular velocity and Mars's angular velocity. To calculate this, we write:
// Starting Planet Angular Velocity Variable angVelStarting = (360/(2 * Pi)) * sqrt(Sun.Mu/(startingOrbit^3)); // Phase Angular Velocity Variable angVelPhase = angVelStarting - angVelTarget; |
Now that we have the phase angular velocity, we can calculate how long it will take until we've reached our departure position. To calculate this, we take the difference of our current phase angle, and our departure phase angle. If we divide this difference by the phase angular velocity, we will have the amount of time (in seconds) until we've reached our departure position. Then, we can add that to our current epoch to calculate the departure epoch. To do this, we write:
// Time until Departure Variable timeTilDep = (currentPhaseAngle - phaseAngle)/angVelPhase; // Departure Epoch TimeSpan departureEpoch = InterplanetarySC.Epoch + TimeSpan.FromSeconds(timeTilDep); |
We have done all the necessary calculations for our first maneuver. Now, we need to step to the departure date, maneuver, then step to the arrival date. Let's go back to the Mission Sequence.
•Drag and drop a FreeForm script editor after the 'Calculate Phase Angle' FreeForm
•Open the script editor and rename it to 'Step to Departure, Maneuver, Step to Arrival'
In this script, we will step to the departure epoch, maneuver the Spacecraft, change the Spacecraft tail color for a better visualization, calculate the arrival epoch, and step to the arrival epoch. To do this, we write:
// Steps to the departure time While(InterplanetarySC.Epoch < departureEpoch); Step InterplanetarySC; Step MarsSC; Update ViewWindow1; End; // Maneuvers the spacecraft for the Hohmann transfer Maneuver InterplanetarySC using ImpulsiveBurn1; // Changes the tail color of the spacecraft InterplanetarySC.Color = ColorTools.Cyan; // Arrival Epoch TimeSpan arrivalEpoch = InterplanetarySC.Epoch + TimeSpan.FromSeconds((1/2)*(THoh)); // Step to Arrival While(InterplanetarySC.Epoch < arrivalEpoch); Step InterplanetarySC; Step MarsSC; Update ViewWindow1; End; |
The last thing we need to do for this transfer is to match our speed with our target. Let's go back to the Mission Sequence.
•Drag and drop a FreeForm script editor after the 'Step to Departure, Maneuver, Step to Arrival' FreeForm
•Open the script editor and rename it to 'Orbit Matching Maneuver'
In this script, we will need to calculate speed of Mars's orbit, calculate the Δv required to match the orbit, maneuver the spacecraft, then propagate for 300 days to visualize this change. To do this, we write:
// Velocity of Mars orbit Keith sweat free music downloadzerodigital. Variable vMarsOrbit = sqrt(Sun.Mu * ((2/arrivalOrbit) - (1/arrivalOrbit))); // Delta V required for maneuver Variable dV2 = vMarsOrbit - InterplanetarySC.VMag; ImpulsiveBurn1.BurnDirection[0] = dV2; Maneuver InterplanetarySC using ImpulsiveBurn1; // Propagates SC for 300 days While(InterplanetarySC.ElapsedTime < TIMESPAN(300 days)); Step InterplanetarySC; Step MarsSC to (MarsSC.Epoch InterplanetarySC.Epoch); Update ViewWindow1; End; |
One more thing we need to add to the script - the thing we've been looking for all along! We need to report the Δv, and the time of flight in days. For the time of flight, we can simply take the difference of the arrival epoch and the departure epoch as these are measured in days. To report these values, we write:
Report (dV1 + abs(dV2)), (arrivalEpoch - departureEpoch).ToDays(); |
Your Mission Sequence should look something like this:
Mission Sequence Example
Save and run your Mission Plan, then try and answer these questions:
How much total Δv was required for the transfer?
How many days did the transfer take? Graphics card serial number lookupmilkwestern.
Try reporting the distance between the two spacecraft at the time where InterplanetarySC 'meets' MarsSC (right before the orbit matching maneuver). To do this, you can add the command 'Report InterplanetarySC.RadialSeparation(MarsSC)' right before the command to perform the second maneuver. About how far apart were the Spacecraft?
See Also
•Interplanetary Topics
•Next Topic: Patched Conics Transfer
STK Professional, Astrogator
You can obtain the necessary license for the training by visiting http://licensing.agi.com/stk/evaluation or contacting AGI Support at support@agi.com or 1-800-924-7244.
The results of the tutorial may vary depending on the user settings and data enabled (online operations, terrain server, dynamic Earth data, etc.). It is acceptable to have different results.
Watch the following video, then follow the steps below incorporating the systems and missions you work on (sample inputs provided).The Hohmann Transfer is, in terms of the velocity change (Delta-V) required, the most efficient two-burn method of transferring between two circular, coplanar orbits. As shown in the illustration, a Hohmann Transfer uses an elliptical transfer orbit with its periapsis at the inner orbit and its apoapsis at the outer orbit.
In the following exercise the purpose is to transfer a satellite from a low-Earth parking orbit with a radius of 6700 km to an outer circular orbit with a radius of 42,238 km.
This exercise and the one that follows are based on Example 3-6-1 in Hale, Francis J., Introduction to Space Flight, Englewood Cliffs, N.J.: Prentice-Hall (1994), pp. 43-44.
The values used here for the radii of the inner and outer orbits are for illustration purposes only. For further practice after completing this exercise, try substituting different values, such as a radius of 42,164.197 km (geosynchronous) for the outer orbit.
Setup
- Create a scenario.
- Set the analysis period to the following:
Option Value Analysis Start Time 1 Jul 2016 16:00:00.000 UTCG Analysis End Time 2 Jul 2016 16:00:00.000 UTCG - Insert a satellite () using the Define Properties () method.
- Re-name it Hohmann_Sat.
- On the Orbit page, select the Astrogator propagator. You may need to expand the properties window to see all of the controls.
Constructing the MCS
To design a Hohmann transfer from a 6700 km parking orbit to a 42,238 km outer orbit, you will use the following MCS segments:
- An Initial State defining a parking orbit with a radius of 6700 km
- A segment to Propagate the parking orbit
- An Impulsive Maneuver to enter the elliptical transfer orbit
- A segment to Propagate the transfer orbit to apogee
- An Impulsive Maneuver to enter the outer circular orbit
- A segment to Propagate the outer orbit
Let's take it a step at a time.
Define the Initial State
- The default MCS that appears when you display the satellite's Orbit page probably already begins with an Initial State segment. If not, insert one at the beginning of the MCS.
- Name the segment 'Inner Orbit'.
- Select Keplerian as the Coordinate Type.
- Change Semi-major Axis to Periapsis Radius with a value of 6700 km.
- Click the Fuel Tank tab
- Set Maximum Fuel Mass to 5000 kg.
- Set the Fuel Mass to 5000 kg.
All other elements should be set to zero. Your set up should match the following:
| Field | Value |
|---|---|
| Coordinate Type | Keplerian |
| Periapsis Radius | 6700 km |
| Eccentricity | 0 |
| Inclination | 0 |
| Right Asc. of Asc. Node | 0 |
| Argument of Periapsis | 0 |
| True Anomaly | 0 |
Propagate the Parking Orbit
- If the second segment of the MCS is not already a Propagate segment, insert one in that position. Name it 'Parking Orbit'.
- Select Earth Point Mass as the Propagator.
- If the color currently assigned to the Propagate segment won't show up well on the selected 3D Graphics window background (or you just don't like it), select a different color.
- Set the Duration (Trip value) to 2 hours (7200 sec), more than enough to have the satellite orbit one complete pass.
Maneuver into the Transfer Ellipse
- Insert, as the third segment of the MCS, a Maneuver.
- Name the segment DV1.
- The Maneuver Type should be set to Impulsive by default. If it is not, select that option.
- On the Attitude tab, select Thrust Vector in the Attitude Control field.
- Select VNC(Earth) in the Thrust Axes field.
- Select the Cartesian option.
- Set the X (Velocity) component to 2,421 m/sec. This will apply all the Delta-V in the thrust direction.
- Click the Engine tab and select the Update Mass Based on Fuel Usage check box.
Propagate the Transfer Orbit to Apogee
- Insert, as the fourth segment of the MCS, another Propagate segment.
- Name the segment 'Transfer Ellipse' and select a color that will distinguish it from the first Propagate segment.
- Select Earth Point Mass as the Propagator.
- Insert an Apoapsis Stopping Condition and remove Duration.
Maneuver into the Outer Orbit
- Insert, as the fifth segment of the MCS, another Maneuver.
- Name the segment 'DV2'.
- Again, the Maneuver Type should be set to Impulsive.
- On the Attitude page, select Thrust Vector in the Attitude Control field.
- Select VNC(Earth) in the Thrust Axes field.
- Select Cartesian as the vector type.
- Set the X (Velocity) component to 1,465 m/sec.
- On the Engine page, select the Update Mass Based on Fuel Usage check box.
Propagate the Outer Orbit
- Insert, as the final segment of the MCS, a Propagate segment.
- Name the segment 'Outer Orbit' and select a color that will distinguish it from the other two Propagate segments.
- Select Earth Point Mass as the Propagator.
- Set the Duration to 24 hours (86400 sec), so that the satellite will make a complete orbit pass (and one will be drawn in the 3D Graphics window).
Hohmann Transfer Calculator
The MCS tree should appear as follows when you are finished:
Running and Analyzing the MCS
Run the MCS. Select the 3D Graphics window, and adjust the view so that you can see the entire ephemeris by orienting it from the north or south pole of the Earth and then zooming out. The ephemeris displayed in the window should be similar to the illustration (except that the inner orbit is closer to the central body). The parking orbit, transfer trajectory and outer orbit should be clearly differentiated by the colors you selected for the three Propagate segments.
If the Propagate segments do not display in the selected colors, open the MCS Options window and make certain that the Draw Trajectory in 3D as it is Calculated and Use Trajectory Segment Colors options are selected.
Hohmann Transfer Maneuvers
If you highlight the last Propagate segment ('Outer Orbit') and create a Summary report, you'll find that the semimajor axis of the outer orbit is very close to the desired value of 42,238 km. Also check the final Fuel Mass. As you'll recall, in defining the Initial State, you set Fuel Mass to 5000 kg, and, in setting up the two Impulsive Maneuvers, you opted to have mass decremented on the basis of fuel usage. If you highlight the second Propagate segment (after the first Delta-V but before the second), you'll find a value for Fuel Mass between the initial and final values.
